Kryptografia dostarcza narzędzia dzięki którym można, stosując metody matematyczne, zabezpieczać zarówno dane gromadzone w lokalnych magazynach informacji jak i dane przesyłane przez sieć.
Szyfrowanie informacji ma szczególne znaczenie, jeśli korzystamy z systemów otwartych takich jak na przykład Internet. Rozwój bezpiecznych metod kryptograficznych w znaczący sposób przyczynił się do rozwoju handlu elektronicznego i bankowości elektronicznej.
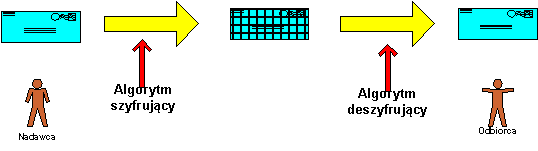
Szyfrowanie jest metodą powszechnie stosowaną do ochrony informacji. Choć metody szyfrowania zmieniały się na przestrzeni wieków, to ogólny mechanizm wygląda ciągle tak samo. Można go przedstawić w następujący sposób:
Proces szyfrowania i deszyfrowania
Aby można było stosować opisaną powyżej metodę do bezpiecznego przesyłania informacji, to odczytanie tekstu zaszyfrowanego bez znajomości algorytmu deszyfrującego powinno być bardzo trudne lub niemożliwe. Istnieje wiele metod spełniających te wymaganie. Najpopularniejsze z nich i najczęściej stosowane to szyfrowanie z kluczem tajnym i szyfrowanie z kluczem publicznym.
W szyfrowaniu z kluczem prywatnym (tajnym) zarówno odbiorca jak i nadawca posługują się tajnym kluczem służącym do szyfrowania i deszyfrowania wiadomości. Z tego powodu tego typu postępowanie nosi również nazwę szyfrowania symetrycznego.
Aby można było stosować tę metodę komunikacji muszą być dostępne następujące elementy:
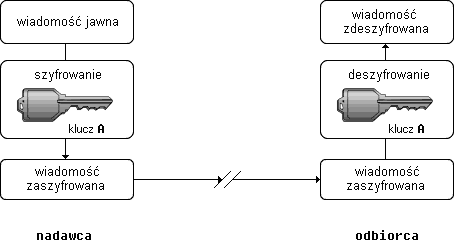
Szyfrowanie z kluczem prywatnym (symetryczne)
Klucze prywatne są powszechnie stosowane przez protokoły bezpieczeństwa, jako klucze sesji w poufnej komunikacji w trybie on-line. Na przykład protokół IPSec wykorzystuje symetryczne klucze sesji ze standardowymi algorytmami stosowanymi do szyfrowania i deszyfrowania poufnej komunikacji między stronami. Dla każdej poufnej sesji komunikacji używane są inne klucze.
Szyfrowanie symetryczne jest też powszechnie stosowane przez technologie zapewniające masowe szyfrowanie trwałych danych, takich jak wiadomości e-mail czy pliki typu dokument. Protokół S/MIME stosuje klucze symetryczne do szyfrowania wiadomości poufnej poczty, a system szyfrowania plików EFS w Windows 2000/XP używa symetrycznych kluczy do szyfrowania plików.
Powszechnie wykorzystywanym, symetrycznym algorytmem szyfrującym jest algorytm DES (ang. data-encryption standard), który w ogólnych założeniach wygląda następująco:
Jeśli przez Ek oznaczymy algorytm szyfrowania z kluczem k, a przez Dk – algorytm deszyfrowania z tym kluczem, to wówczas dla każdej wiadomości m muszą być spełnione następujące warunki:
1) Dk(Ek(m))=m – oznacza to, że po zaszyfrowaniu wiadomości (Ek(m)) przesłaniu jej, a następnie odszyfrowaniu (Dk(Ek(m))) nie zgubimy informacji, czyli że proces szyfrowania i deszyfrowania nie zniekształca wiadomości;
2) Obliczenie Ek i Dk jest efektywne, czyli daje się wykonać w rozsądnym czasie przy zastosowaniu dostępnym zasobów obliczeniowych;
3) Bezpieczeństwo systemu zależy tylko od tajności klucza k, a nie od tajności algorytmów E i D - – oznacza to, że algorytmy szyfrowania (E) i deszyfrowania (D) mogą być ujawnione, a chronić należy jedynie wartość klucza k.
Szczegółowy opis działania algorytmu DES wykracza poza zakres tego wykładu.
Gwałtowny wzrost mocy obliczeniowej komputerów doprowadził do tego, że obecnie algorytm DES można złamać w ciągu zaledwie kilku godzin. Dlatego opracowany został algorytm 3-DES (Triple DES), w którym zwiększone bezpieczeństwo uzyskano poprzez zastosowanie dwóch lub trzech kluczy. Dzięki zastosowaniu 3-DES czas potrzebny na złamanie szyfru znacząco się wydłuża – na dzień dzisiejszy liczony jest w milionach lat.
Problemem w szyfrowaniu symetrycznym jest przekazywanie kluczy. Aby zapewnić bezpieczeństwo informacji klucz taki musi pozostać tajny. Nie może więc być bezpośrednio przesłany przez sieć telekomunikacyjną, gdyż byłby narażony na łatwe przechwycenie.
Problem ten rozwiązano poprzez szyfrowanie z wykorzystaniem różnych kluczy do szyfrowania i deszyfrowania. Ten sposób szyfrowania nosi nazwę szyfrowania asymetrycznego (lub publicznego). Polega on na zastosowaniu dwu kluczy: jednego do szyfrowania wiadomości, a drugiego do deszyfrowania.
W szyfrowaniu z kluczem publicznym każdy użytkownik dysponuje dwoma kluczami. Jeden z nich to klucz jawny służący do szyfrowania wiadomości. Drugi to klucz tajny, znany tylko odbiorcy wiadomości. Służy on do odszyfrowania wiadomości.
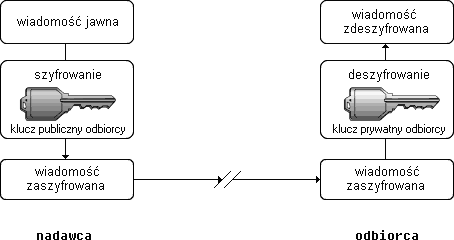
Szyfrowanie asymetryczne
Dwaj użytkownicy mogą się skutecznie porozumiewać znając swoje klucze jawne.
Zasada działania algorytmu szyfrowania opartego na kluczach prywatnych bazuje na własnościach matematycznych dużych liczb. Polega ona na tym, że mnożenie dwu nawet dużych, specjalnie dobranych liczb jest łatwe. Trudne jest natomiast wykonanie rozkładu liczby na czynniki (o ile liczba jest odpowiednio duża i dobrze dobrana). Oznacza to, że odszyfrowanie wiadomości bez znajomości klucza tajnego wymaga ogromnych mocy obliczeniowych (a co za tym idzie czasu) lub jest niewykonalne.
Najbardziej
popularnym algorytmem z kluczem publicznym jest algorytm RSA opracowanym przez
Ronalda Rivesta, Adi Shamira i Leonarda Adlemana. Bazuje on na trudności rozłożenia
dużej liczby na czynniki pierwsze. Wykorzystuje funkcję Eulera Totient
zdefiniowaną jako ilość liczb
naturalnych mniejszych od n i względnie pierwszych z n. Liczby m
i n są względnie pierwszymi, jeśli nie mają wspólnych podzielników
innych niż 1. Funkcja
zawsze przyjmuje wartość mniejszą
niż n. Euler odkrył, że każda liczba k, względnie pierwsza z n
podniesiona do potęgi
modulo n daje w wyniku 1:
(a mod b oznacza resztę z dzielenia liczby a przez b. Na przykład 10 mod 3 =1; 4 mod 2 = 0)
W RSA wykorzystuje się jeszcze jedną własność. Jeżeli k
i l są losowymi liczbami naturalnymi będącymi odwrotnościami modulo
oraz A jest dowolną liczbą
względnie pierwszą z n to:
.
Jeśli
A jest częścią wiadomości wówczas szyfrowania dokonujemy za pomocą
funkcji
,
zaś
deszyfrowania za pomocą funkcji
.
Wyboru kluczy szyfrujących dokonuje się w następujący sposób:
·
losuje się dwie duże liczby pierwsze p, q;
·
oblicza się n = pq, oraz wyznacza funkcję
;
·
losowo wybiera się liczbę e z przedziału
(1,
), względnie pierwszą z
;
·
wyznacza się liczbę d odwrotną do
, czyli
;
·
kluczami szyfrującymi są k = (n, e) oraz l
= (n, d).
Dysponując kluczami szyfrujemy wiadomość A.
W algorytmie
RSA liczby n oraz k lub l można wyjawiać bez poważnego
narażenia bezpieczeństwa. Do złamania szyfru potrzebna jest funkcja
zaś do jej znalezienia musimy rozłożyć
n na czynniki pierwsze, co jest zadaniem bardzo trudnym. W praktyce
stosuje się klucze o długości 512–1024 bitów. W 1999 roku rozkład na
czynniki pierwsze liczby 512-bitowej zajął trzystu szybkim stacjom około
siedmiu miesięcy. Dlatego klucze o takiej długości nie stanowią obecnie
dobrego zabezpieczenia.
W praktyce często stosuje się połączenie metody szyfrowania symetrycznego i asymetrycznego. Ponieważ szyfracja i deszyfracja wiadomości przy użycia klucza prywatnego jest dużo szybsza niż przy stosowaniu klucza publicznego, więc przy komunikacji dwu stron stosuje się następującą metodę. Klucze prywatne nadawcy i odbiorcy przekazuje się stosując metodę szyfrowania z kluczem publicznym. Klucz taki może więc być bezpiecznie przekazany przez publiczną sieć telekomunikacyjną. Następnie wiadomości mogą być już przekazywane przy zastosowaniu szyfrowania metodą klucza prywatnego.
Każdy z rozmówców generuje fragment klucza prywatnego i przed przesłaniem do partnera szyfruje go stosując metodę szyfrowania z kluczem publicznym.
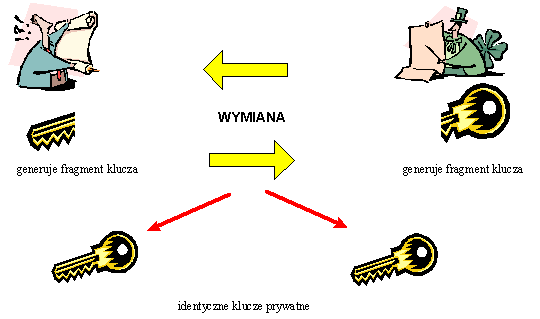
Wymiana kluczy prywatnych
Przykłady szyfrów